Dot Paper Task

A low-tech task with high-level thinking

I’m a guest teacher in a 4th-grade classroom. Each desk already has a sheet of dot paper, same as the one I place under the document camera for me to use.

“Please draw what I draw,” I tell them.

Me: What did we just draw?
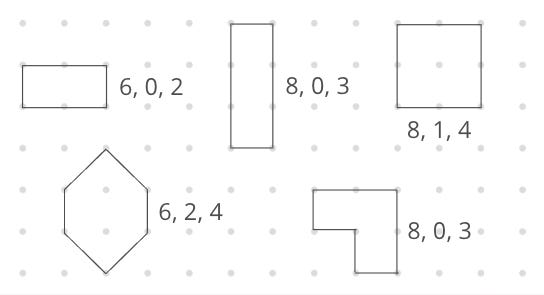
Them: A rectangle!
Me: Yes, a rectangle. But today, I’m giving it a new name. I’m calling it “6, 0, 2.” Please write that next to your sketch.

Me: Let’s draw another… And I’m naming this one “8, 0, 3.”

I ask them to notice and wonder how I’m naming the shapes, but to keep their thoughts to themselves so everyone can think. A few muffled oohs and ahhs escape. I thank them for holding onto their ideas.

By the time we draw five shapes, they figure it out: the first number is the border dots, the second is the inside dots, and the third is the area.

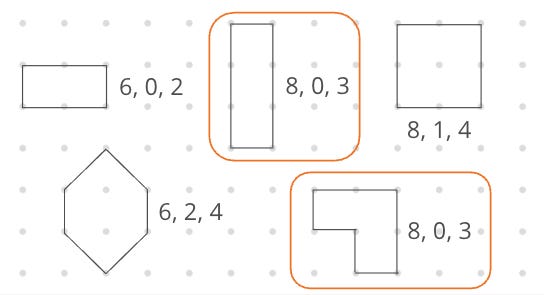
I circle two shapes that have the same “name” but look different. “Can you draw a different one that still has the same name?” We talk about what “different” means and agree: if two shapes can overlap exactly, they’re not different.

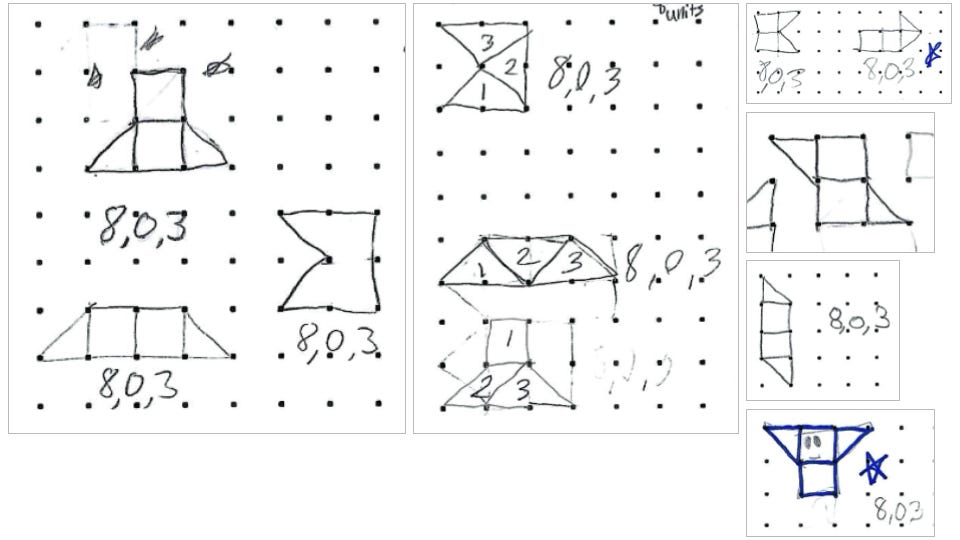
Below is my actual dot paper—I’m sketching freehand as we go.

They rise to the challenge. That bottom-right sketch? Also called “Baby Yoda.”

Without any prompting from me, notice how they partition their shapes into smaller chunks to make sure they have the correct square units.

For most of the class, students create their own shapes and name them. I ask them to challenge a partner in two ways:

1. Cover the name and ask the partner to figure it out.

2. Show only the name and ask the partner to draw it.

They quickly agree the second way is tougher.

With about 15 minutes left, I get their attention. “I see lots of shapes on your paper, so I think we’re ready for me to show off. Raise your hand and give me just the first two numbers of your shape. I’ll write them in a table—B for border, I for inside. That’s all I want. I’ll figure out A, the area.” We fill in the table one row at a time.

It’s not easy to impress 4th graders, but I seem to be pulling it off. A few exclaim, “How did you figure that out?!”

I encourage them, “Well, how am I figuring it out? Keep giving me more sets so we can fill out the table and look for patterns.”

They are fully engaged—curious, thoughtful, collaborating.

Then comes the best moment of the day. One student raises her hand and says, “Can we just focus on the sets that have I = 0?”

I mean. That’s a pro move. That’s exactly what we should do when juggling multiple variables—ignore some. What she suggests is what my math hero Joshua Zucker calls wishful thinking. Yeah, let’s wish away the inside dots for now.

Within minutes, several students notice a relationship between B and A [when I = 0].

The class is winding down when one student raises his hand and says, “I have a big challenge for you.”

“Sure,” I say.

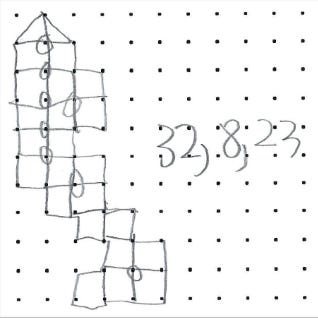
He yells out, “32 and 8,” and I ask, “You drew this shape?” He nods, dead serious. I do my mental calculation—slowly and carefully, because I’ll be damned if I lose to a 4th grader in front of everyone.

Finally, I write down the value for the area.

He stands up: “Ugh! How did you do that!”

Here’s his paper.

The bell has already rung. I thank them for their perseverance and for playing along. They file out.

The teacher comes over to me and says, “Fawn, that kid is going to spend the next three nights trying to figure out how you did that.”