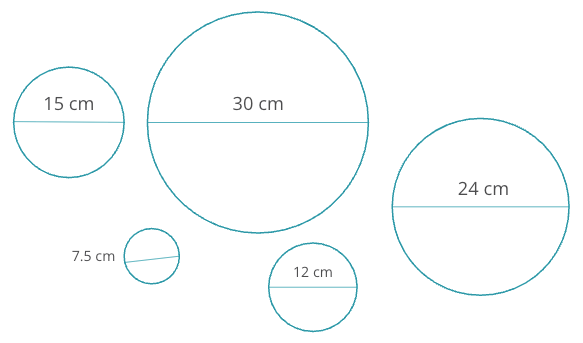
More recently, during a talk, I asked attendees to recall how we find the mean or average. For example, if we needed the mean diameter of a set of circles, no problem—we’d just add them up and divide.
Then I gave them this problem:
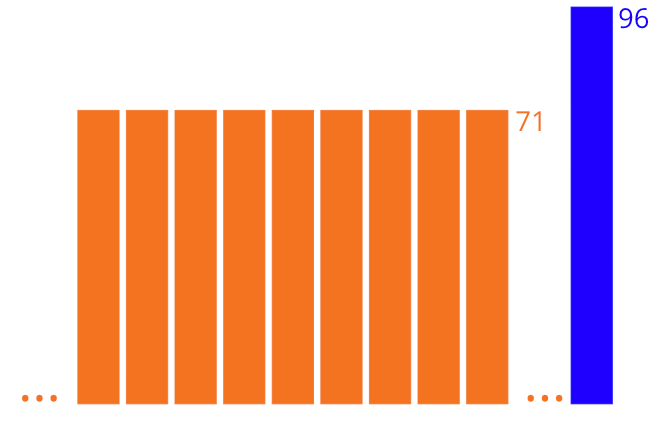
Tamisha was ill and had to take a test a day late. Her score of 96 raised the class average from 71 to 72. How many students, including Tamisha, took the test?
If you’d like, go ahead and work on the problem before reading on.
-
-
-
-
-
-
-
-
-
-
-
-
I’ve observed most teachers go straight to algebra.
But how would a kid without equation-writing finesse tackle this?
Here’s where conceptual understanding edges out computational firepower.
Too often, “finding the mean” gets treated like this:
Or, we make paper chains. Or, football is added because… motivation?




This is where having a high-quality curriculum matters. Amplify Desmos Math has an army of thoughtful, grounded, and curious people who take this work so very seriously.
In 2nd and 3rd grade, students spend a lot of time thinking about equal sharing and grouping. The problem below gives meaningful context, and the visual model makes the idea concrete and especially powerful:
Then, in 6th grade, students build on this foundation to find the mean.
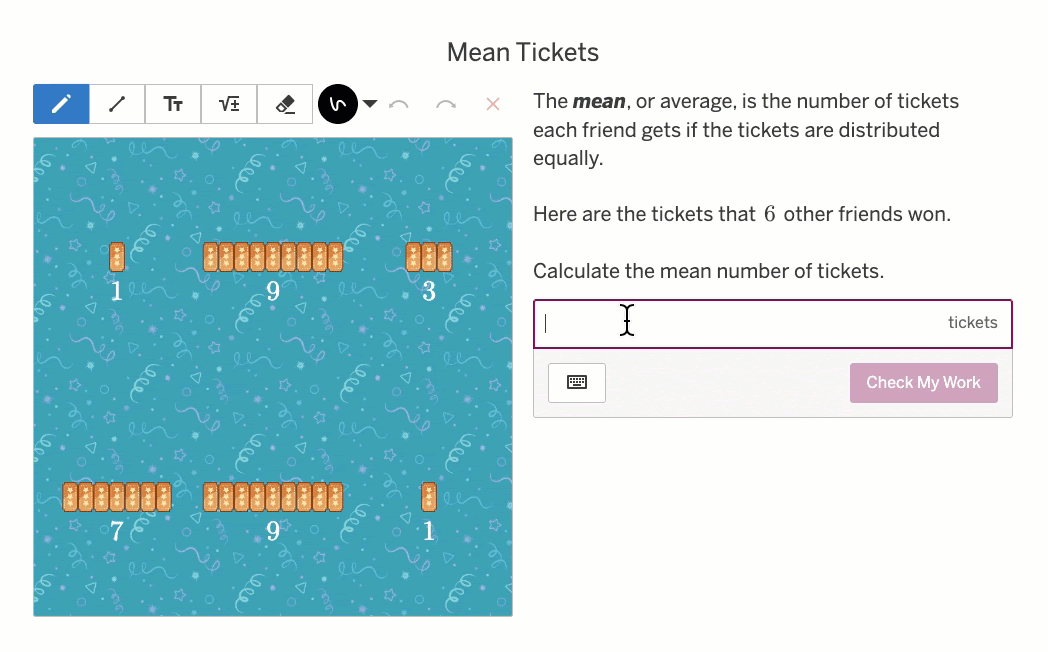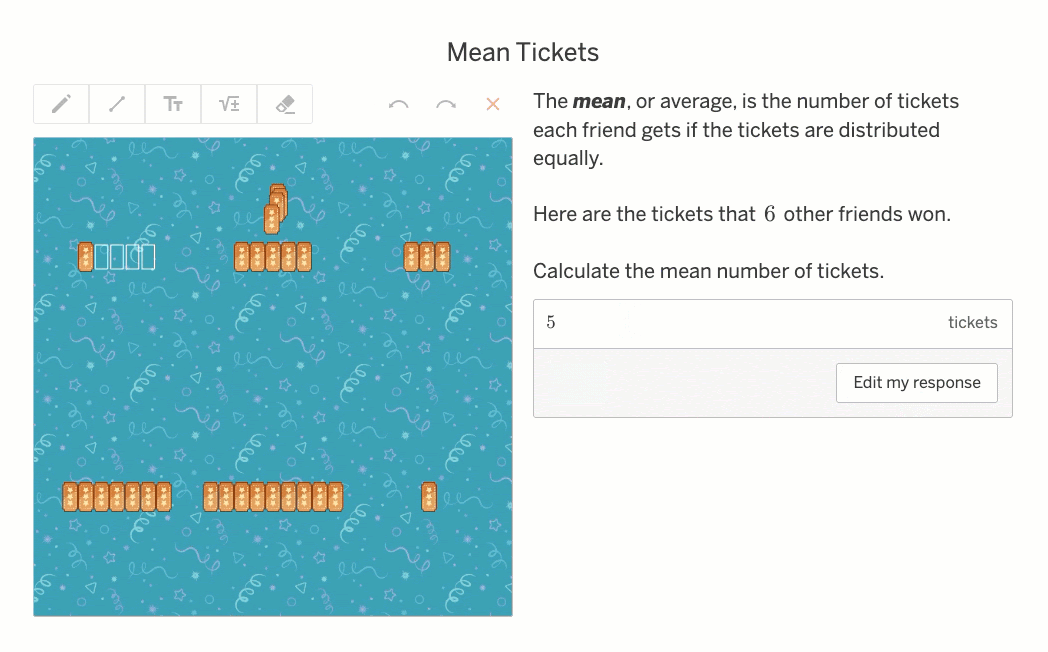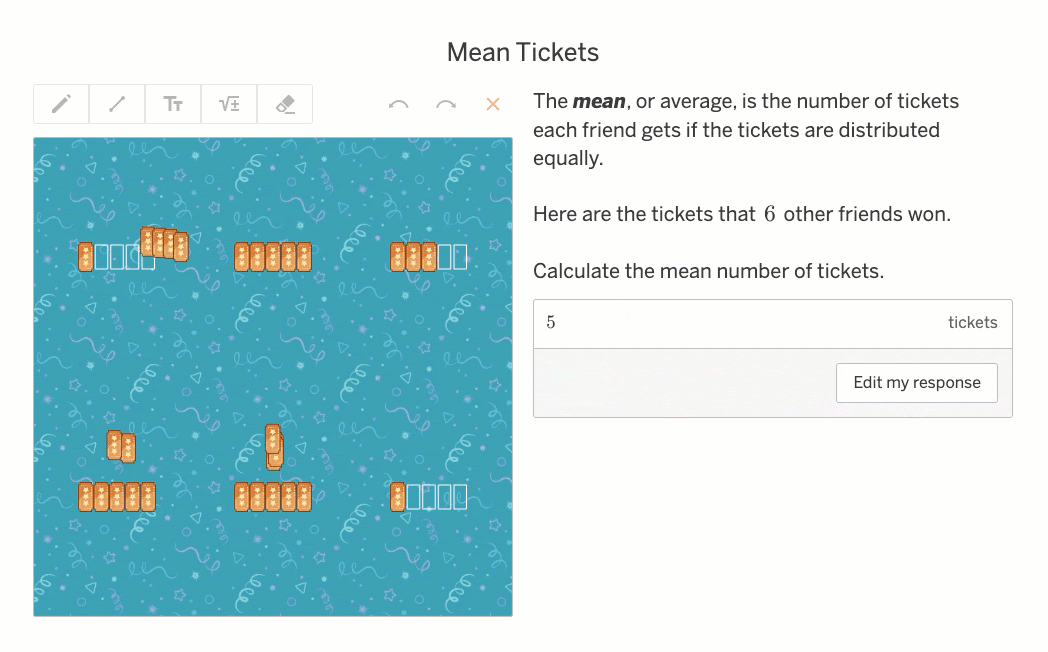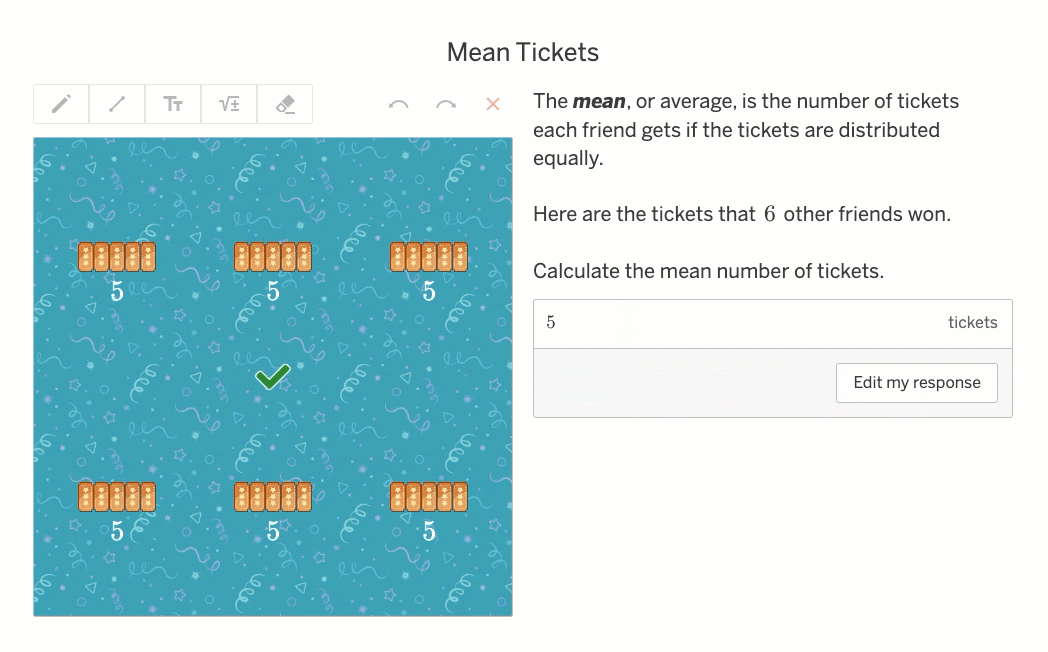
When I enter an incorrect answer of 13, I get feedback showing five leftover grapes—so I know each friend can get one more. The correct answer is 14 grapes.
We’re not just telling students what the mean is. Yes, we define it clearly: “The mean, or average, is the number of tickets each friend gets if the tickets are distributed equally.”
But more importantly—we’re showing it. I can see the equal groups.
So now, back to Tamisha.
You probably know by now that I see rectangles everywhere in math. When I think of the mean, I picture a stack of rectangles, all the same height. Here’s my mental image of the mean score of 71:
Then Tamisha scores 96…
She must have distributed her extra points to her classmates, raising everyone’s bar to 72.
This problem only required subtraction.
Just because we can use algebra doesn’t mean we have to.
The more we embed visual representations into concept development, the more we help students build intuition, not just follow steps.







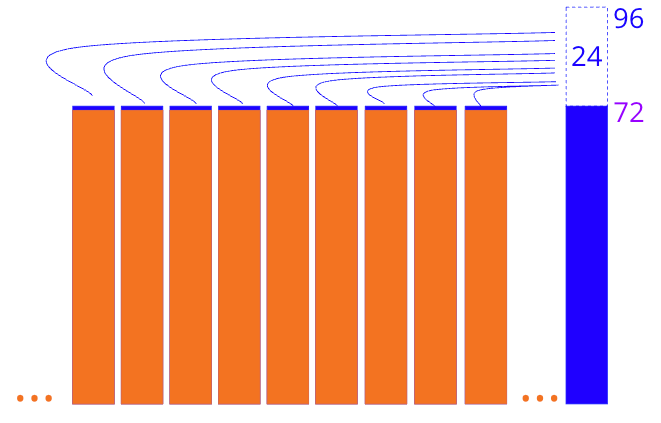
Elegant!