On the first day of school, I promised my students that I’d do my best to make math relevant and challenging. I also promised I’d never waste their time — which meant we would be doing math every single day, including the last one.
I did not promise that math would be fun. Math is already fun — to me. I’ve handed out math puzzles at birthday parties, baby showers, and yes, even my own wedding.
Math 6: How Many Regions?
(Adapted from AIMS)
Each student got a 4-by-4-inch paper square and a few thin 6-inch paper strips — each strip would represent a "cut."
What’s the maximum number of regions you can divide the square into using n cuts?
We did the first two cuts together and recorded data in journals.
Kids quickly realized the cuts must intersect to maximize regions. Two non-intersecting cuts gave just 3 regions. One student yelled out,"Parallel cuts!" Gotta love when kids blurt out academic language.
This class had worked with pattern worksheets nearly every Monday, so recursive rules came naturally. They noticed that for any n, the maximum number of regions is the previous number of regions plus n.
With 30 seconds left of class, I told them my parting gift was a challenge: Can you figure out the equation?
Matt asked, "Can I email you over the summer?"
Yes. Yes, you can.
Algebra 1: 2012 Clocks
Our 8th graders' last day of classes was yesterday (Wednesday). They’ll return tonight for their promotional ceremony, all dressed up.
I needed a quick one-period lesson, so we made 2012 Clocks — a classic challenge:
Using the digits in 2012 (once each), create expressions equal to the numbers 1 through 12 — the hours on a clock.
Geometry: Desert Crossing
(Also from AIMS)
This one’s a favorite. (I first saw it as a camel and banana problem, but I prefer watermelons.)
The scenario:
You live at an oasis and grow miniature watermelons, worth a fortune if you can get them to market — 15 kilometers across the desert.
You have 45 melons.
Your backpack holds 15 melons max.
You consume 1 melon per kilometer walked, whether going forward or returning.
Challenge: Get as many melons to market as possible.
As I write this, Slater doesn’t know I’m awarding him the Math Excellence Award at tonight’s ceremony.
Here’s his work — one way to arrive at the correct answer: 8 melons.
A few weeks ago, we also did a quick volume demo.
Each student constructed two rectangular prisms from identical paper.
(Dan Meyer folds them into cylinders, but we stayed rectangular.)
The question:
Pretend each has a bottom. Which one holds more popcorn?
I asked them to take a look — then pick up the one they thought held more. Or both, if they thought the volumes were equal.
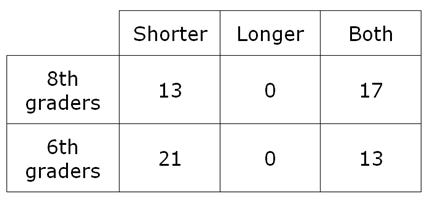
Here’s what they grabbed:
Then they measured and calculated volume.
Favorite student quote: “The tallness didn’t make up for the fatness.”
Estimating volume is a funny thing.