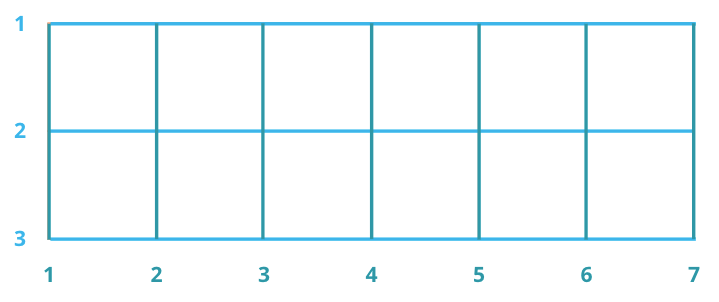
I’m with 6 graders today. I ask them to draw a 2 by 6 rectangle like this on grid paper:
How many lines or segments do you see?
Yes—3 horizontal and 7 vertical—so this rectangle has 10 lines total.
How many squares do you see?
Ah, yes. There are 12 small ones and five 2x2 ones, for a total of 17 squares.
Now that we’re all on the same page about how we’re counting lines and squares, here’s another one: a 3 by 4 rectangle.
I’ll just tell you—it has 9 lines and 20 squares. Trust me, bruh.
My challenge for you:
Can you draw a rectangle that uses the fewest number of lines and has exactly 100 squares?
Insanely good thinking, reasoning, and persistence from these students.
Toward the end of class, two groups found the answer. So I asked if they could generalize the problem:
How many lines and squares are in an n by m rectangle?
I wrapped up by flashing them a quick peek at my own work—starting with scribbles on a small notepad, then several pages of graph paper I worked on in my own time, and eventually a spreadsheet—just to show how much I enjoyed this task and wanted to share it with them.
I learned this task from Cathy Williams’s session on the California Math Framework.



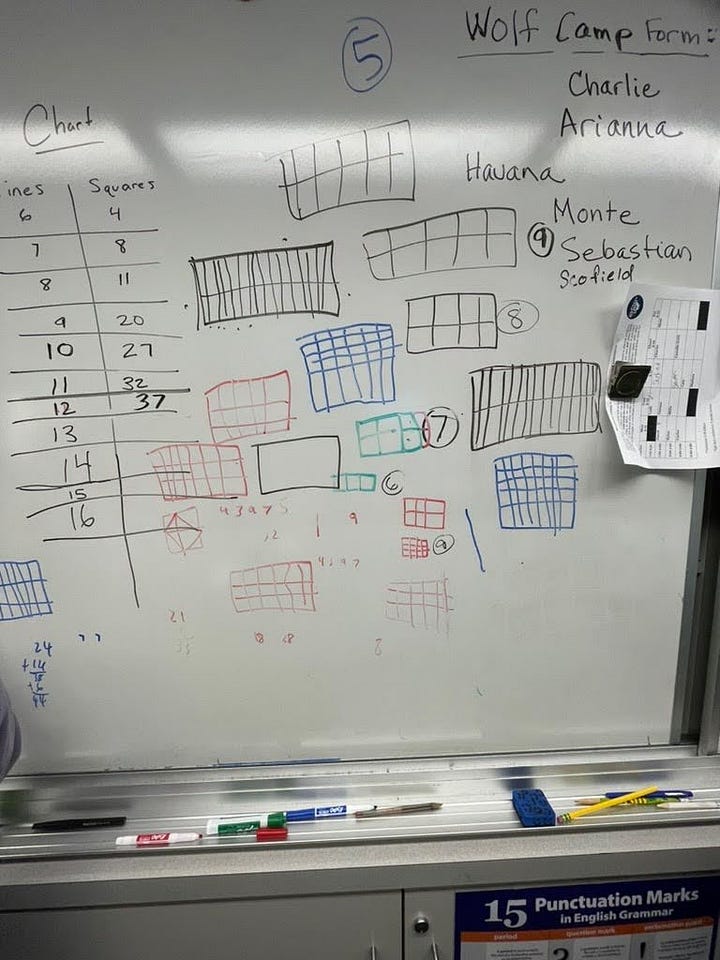
[Added: June 6, 2025]
Never pegged Benjamin Dickman as a show-off, but then he casually drops this 3D Desmos gem: https://www.desmos.com/3d/mekzkazcec