I don't often share what goes through my head when I sit down to plan a lesson. So here it is—what I notice, what I wonder, and what I'd do with it. Whatever curriculum you're using, take what resonates, leave what doesn't.
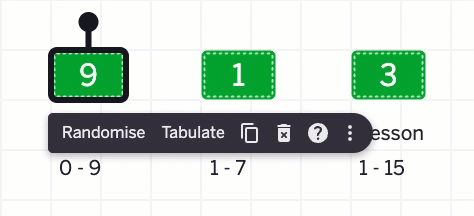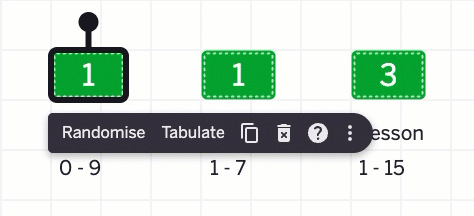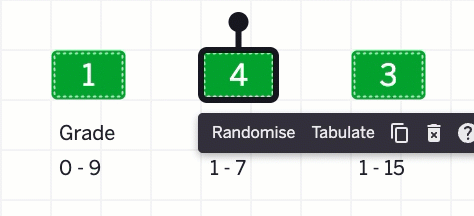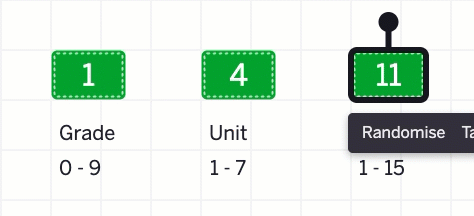
I used Polypad’s Random Number generator to find a lesson from Amplify Desmos Math (ADM) to share how’d I facilitate it. I didn’t want to just cherry-pick one of my favorites. If a curriculum is worth its salt, you should be able to pull any lesson at random and it holds up.
It landed on Grade 1, Unit 4, Lesson 11.
Only about 10% of ADM’s K–1 lessons use digital student screens, so it’s no surprise this one uses the print student edition. I’ve looked through a lot of lessons in the curriculum, but I’m not familiar with this one. Perfect.
I immediately go to the Student Edition (SE). The warm-up says “eyes on teacher.” Just last week, a teacher shared that she loved that ADM doesn’t place the warm-up problem on the SE—because then it becomes just another problem students might do on their own, when it’s supposed to be an opener for talking and sharing.
I pull up the Teacher Presentation Screen (TPS) and see this Notice and Wonder routine. (I first thought it was a Which One Doesn’t Belong, but this is first grade.) I notice the 7s and remember how many students still write 7s backward at this age. And yet they dare make fun of my 7 when I write it with a bar across.
I would give students a full minute to quietly notice and wonder, followed by a turn-and-talk with their neighbor. Then I’d call on students to share while I record their thinking on the board. There’s a second TPS with three questions that can be asked sequentially: 1) How are 7 and 17 alike and different? 2) How are 70 and 71 alike and different? and 3) How are 7 and 70 alike and different? Depending on what surfaces from the first slide, I might not need this one.
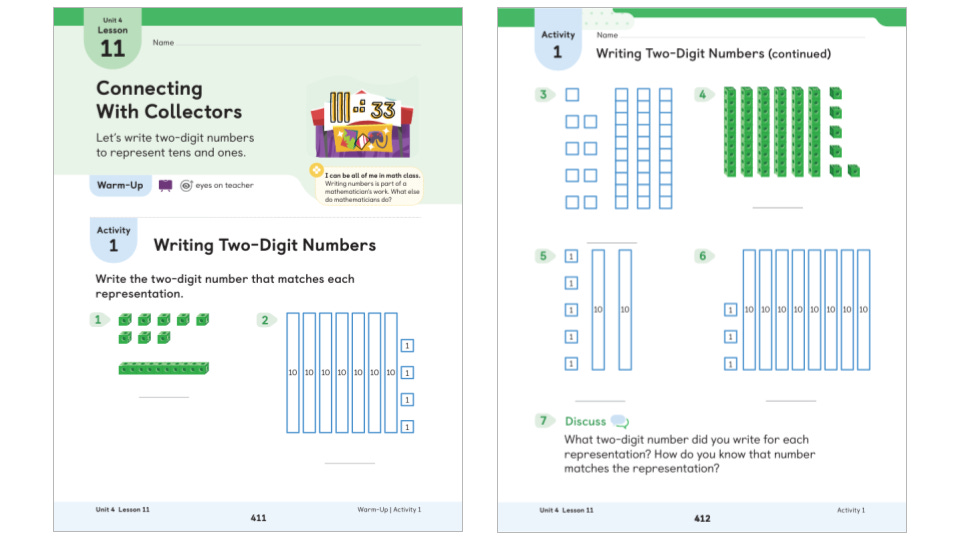
I return to the SE to look at Activity 1. It has seven questions. I notice two different types of representations, but the tens and ones are similar in size in both models. The same green connecting cubes from the warm-up are shown here too. I like that question 3 doesn’t have labels. I answered the questions on a piece of paper and realized that the digits 1–9 are all in the answers. Nice!
I know why these collections are neatly drawn, but I wonder:
If I hand-drew a collection on the board—imperfect tens and ones scattered and lying every which way—how would they count it? Would they count all the tens first? The ones first? Or ten, twenty, twenty-one, twenty-two, thirty-two…?
What if I made a collection of 13 ones and 2 tens? Would someone let me know that I could swap ten ones for one ten?
I don’t remember when coins are taught, but I wonder if it’d be appropriate to pull out pennies and dimes for this. Mental note to check later.
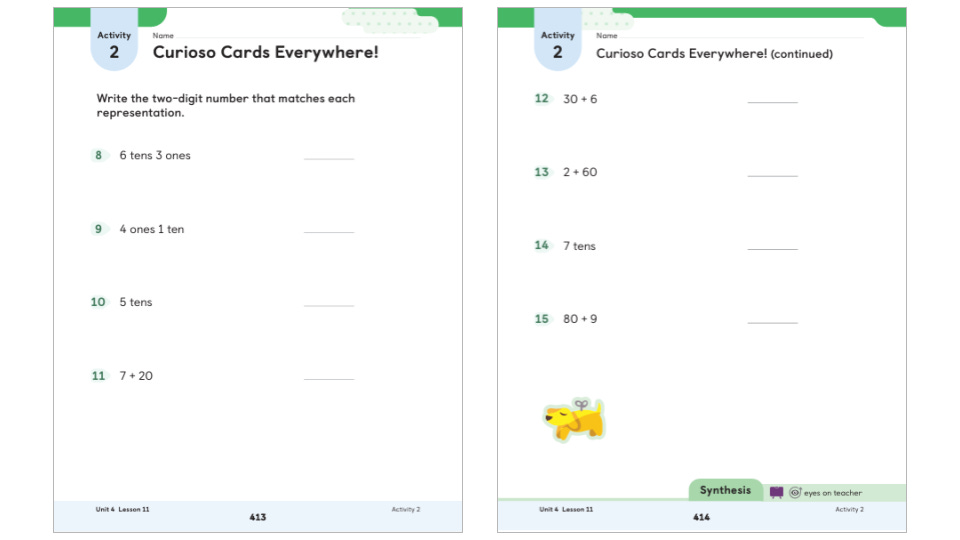
Activity 2 has eight questions. I notice again that students get to practice writing all nine digits if they answer these correctly. I appreciate seeing tens and ones written in different orders. I'm familiar with "Curioso Cards" because they were referenced in the Narrative Unit Story at the beginning of Unit 4.
I’m also thinking:
If I wrote 63 on the board and pointed to the 6 only and asked, “What number is this?” I wonder if they’d say 60 or 6. My plan is if anyone said “six,” I’d respond with, “Hmmm. I don’t see six…”
When I call on students to share their answers for questions 8 through 15, I’d write them in order—vertically or horizontally—without saying anything about it because the number line lives in my head.
Related to above, maybe I’d toss out some comparison questions on the board: Which number is bigger, 30 or 5 tens? What about 60 and 6 tens?
Like the warm-up, the Synthesis at the end of Activity 2 is also “eyes on the teacher.”
Only now do I look at the Teacher Edition (TE).
The reasons I never look at the TE first:
The SE is much shorter. :)
I want to plan from the student experience.
We teach from an asset-based perspective—that students have prior experience, that they have worthy things to bring to the conversation. Well, I know things too, and I want to see if I can bring whatever I’ve got to this lesson. I want to be curious—genuinely curious—while doing some anticipating (à la The 5 Practices) on my own. Seeing stuff before I’m ready to see it tends to ruin everything.
Of course I want to do all the math I’ll be asking my kids to do. It gives me a sense of how long it might take. (Someone once told me that however long it takes you, multiply by 3 and allow that for your students.) The answer key has errors sometimes.
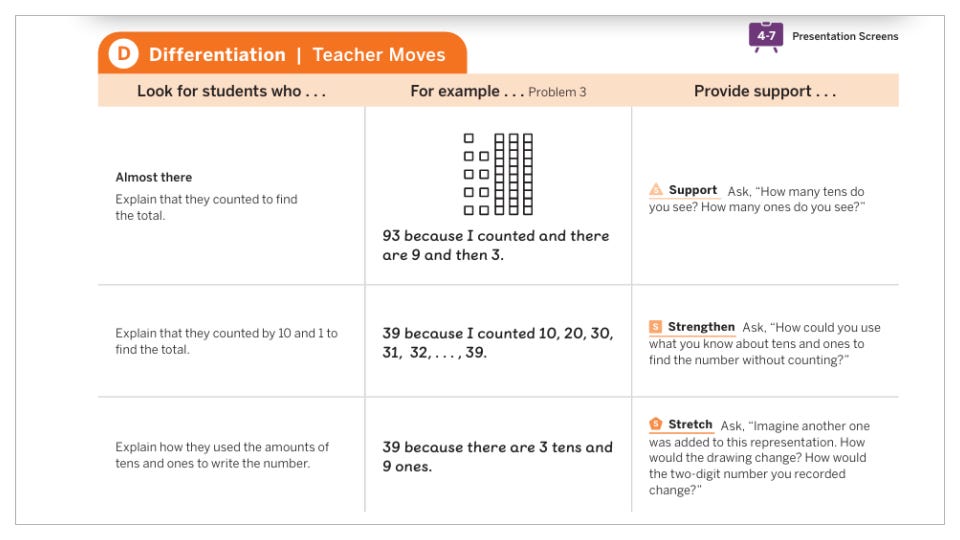
When I finally open the TE, I want it to sharpen what I've already planned and catch what I might have missed—not replace my thinking. Because I'm very familiar with ADM, I already know that there are targeted Differentiation tables throughout a lesson. There are four in this lesson alone. Each one shows what to look for in student thinking and what to do about it. This can be the hardest part of teaching to plan for—and it's just there.
That's about 30 minutes with a lesson I'd never seen before. I'm ready—but what I'm most looking forward to is the thinking I didn't anticipate.