From our textbook:
Stuff like this makes my heart sink. There’s nothing left for students to explore. The problem hands them all the numbers, labels, and even the strategy (“use similar triangles”). Yet the first thing they say is, “I don’t get it.”
They don’t get it because they never got to own it.
So I scrapped the whole thing and handed them a mostly blank page, plus these verbal instructions:
Make sure you have a sharpened pencil. Write your name and date.
Inside this large rectangle, draw a blob—yes, a blob—that takes up about 1/5 of the rectangle’s area.
Now, draw a dot anywhere inside the rectangle but outside the blob. Label it H.
Draw another dot so that there’s no direct path from this dot to H. Label it B.
After some silly guesses, I told them what they had just drawn: a miniature golf course. The blob is water. Point B is the golf ball. Point H is the hole.
The challenge: get the ball into the hole.
Catch: you can’t shoot directly—there’s water in the way. You need a bank shot.
Some blobs and point placements made that impossible, so I let them swap for new sheets. (I kept copies of their originals before they started.)
A student tried a quick solution and asked, “Is this right?” I replied:
“I’m not sure. That’s your challenge. You need to convince me—and your classmates—that your ball will bounce at just the right angle to make it into the hole. What can you draw? What calculations are involved?”
Here’s what I overheard:
“The angle that the ball hits the wall and bounces back must be the same.”
“Because we’re talking about angles… triangles?”
“This is like playing pool.”
“Right triangles.”
“Similar right triangles.”
“Do we need to think about the ball’s velocity?”
“This is hard.”
“I can’t figure out how to use the triangles.”
“Similar triangles make it easier.”
“Even if it bounces more than once, it’s still one hit.”
“I think I got this.”
“I have an idea!”
“Wish my golfer was Happy Gilmore.”
Big struggles. So I stayed out of their way as much as possible. (I was struggling too—and that made them feel better.)
Student highlights:
Lauren explained in a 55-second video how she used proportions and triangle similarity to find her bank shot. She later walked us through her reasoning under the document camera.
From our textbook:
[insert sad excuse for a problem diagram]
Stuff like this makes my heart sink. There’s nothing left for students to explore. The problem hands them all the numbers, labels, and even the strategy (“use similar triangles”). Yet the first thing they say is, “I don’t get it.”
They don’t get it because they never got to own it.
So I scrapped the whole thing and handed them a mostly blank page, plus these verbal instructions:
Make sure you have a sharpened pencil. Write your name and date.
Inside this large rectangle, draw a blob—yes, a blob—that takes up about 1/5 of the rectangle’s area.
Now, draw a dot anywhere inside the rectangle but outside the blob. Label it H.
Draw another dot so that there’s no direct path from this dot to H. Label it B.
After some silly guesses, I told them what they had just drawn: a miniature golf course. The blob is water. Point B is the golf ball. Point H is the hole.
The challenge: get the ball into the hole.
Catch: you can’t shoot directly—there’s water in the way. You need a bank shot.
Some blobs and point placements made that impossible, so I let them swap for new sheets. (I kept copies of their originals before they started.)
A student tried a quick solution and asked, “Is this right?” I replied:
I’m not sure. That’s your challenge. You need to convince me—and your classmates—that your ball will bounce at just the right angle to make it into the hole. What can you draw? What calculations are involved?
Here’s what I overheard:
“The angle that the ball hits the wall and bounces back must be the same.”
“Because we’re talking about angles… triangles?”
“This is like playing pool.”
“Right triangles.”
“Similar right triangles.”
“Do we need to think about the ball’s velocity?”
“This is hard.”
“I can’t figure out how to use the triangles.”
“Similar triangles make it easier.”
“Even if it bounces more than once, it’s still one hit.”
“I think I got this.”
“I have an idea!”
“Wish my golfer was Happy Gilmore.”
Big struggles. So I stayed out of their way as much as possible. (I was struggling too—and that made them feel better.)
Student highlights:
Lauren explained in a 55-second video how she used proportions and triangle similarity to find her bank shot. She later walked us through her reasoning under the document camera.
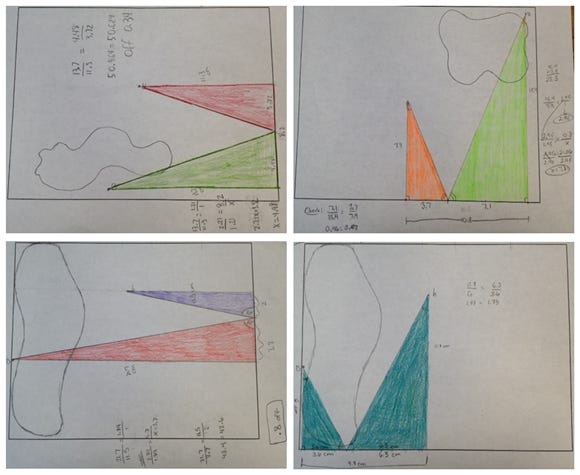
Jack went with the ol’ “eyeball it and adjust” method. He picked an angle that looked right, then tried to preserve the angles with each bounce. (His math wasn’t perfect—90°, 33°, 63°—but the perseverance was there. We’ll work on triangle angle sums another time.)
Gabe was quiet, but when he shared, the room stopped. He had solved the whole problem using only a straightedge and a compass. He showed us how he found the exact bank point C using only constructions—no measurements. It was brilliant.
Imagine if I had just given them problem #24 from the textbook. None of this thinking, sharing, or creativity would’ve happened. Half of the class was still stuck and working by the end—but they were working. And no one said, “I don’t get it.”
Oh, and while all this was happening?
Some students broke into song—to the tune of the Rolling Stones (yes, I told them about the concert we went to over the weekend, and yes, we got escorted into the PIT!!):
🎶 I can’t get no similar triangles
I can’t get no similar triangles
’Cause I try and I try and I try and I try…
I can’t get no, I can’t get no 🎶
I was done. Dead. In love with them all over again.


Update May 8, 2013
Today, students worked on each other’s papers (from the copies I made). Some setups allowed a one-bank solution.
Others didn’t—but I still had them create similar triangles to work through the ideas, because that was the learning goal.

Update June 28, 2014
If I had one post that went “viral,” this was it. There were over 120 comments left for this post on the old site, but I'd like to feature my conversation with Chris (Hillby) as it involves us sharing some geometric constructions.
It turns out Gabe’s hunch was eerily close to a geometric reflection method, like aiming for the reflection of the hole. Chris’s alternate construction was equally beautiful and precise. Gabe didn’t prove it—he just built it, patiently, midpoint by midpoint.














