(I just had my very best lesson yesterday — on a Friday, no less — thank you. I feel almost brilliant right now. And I only feel like this once every 47 years, so please stay and read this post!)
My kids tell me they’ll stock up their dorm rooms and apartments with junk food and soda when they move out, just to make up for all these years of deprivation. (And this is supposed to make me feel bad.) So when I intentionally bring home a snack, like this bag of kettle corn, I usually find it empty within 24 hours. But seeing the empty bag made me think of a volume activity for my 6th graders using all these other bags of Orville Redenbacher popcorn.
The activity I had in mind — maximizing the volume of a box — is usually done in pre-calc or calculus. But these are my 6th-grade babies. Didn’t we do just fine approximating the volume of a torus with my doughnut lesson? So why not this? Besides, I needed to get rid of the popcorn.
I randomly paired them up and gave each pair two sheets of white copy paper. I told them to use one sheet at a time to make a box — the goal was to make the biggest box possible to hold the most popcorn. But it had to be built like this: cut out four corners from the paper, fold up the sides, and tape them. I used a half-sheet (so they couldn’t duplicate mine) to demonstrate.
They quickly got to work. A few groups weren’t cutting square corners, so their box sides didn’t line up. Two groups folded the paper and cut corners, so they had to redo it.
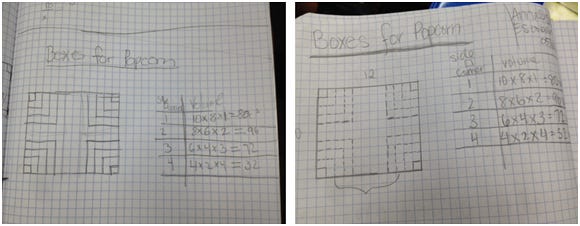
Ryan and Annamaria wanted to make a shallow box. Ryan said, “… it doesn’t matter how high it is.”
Rapha and Cristian made the biggest corner cuts I saw in round one.
Mike and Roy made the shallowest box in class — then changed their minds for box #2.
With 10 minutes left in our first hour, I asked them to measure their boxes and calculate volume. No problem there — we had done the doughnut lesson. They recorded volumes and I tacked them to the board. (Butter seeped through a few of the boxes.)
That was fun. I pointed out that two of the bigger boxes were over 1,000 cubic centimeters. The bell rang. I said, “We’ll wrap up this afternoon.”
Except I had no idea how we were going to wrap up. Also, my microwave overheated and my room reeked of greasy popcorn.
But I had a feeling the kids would help figure out the next step.
In the afternoon, I asked what they’d learned. They said:
The four corners must be the same size. (I never told them this.)
Each corner must be a square. (I didn’t tell them this either. Not everyone believed it, so I cut non-square corners to show them.)
There’s a limit to how big the square can be. (I loved this. It led to the question: Is there a minimum size? One kid said, “No. Technically, no.”)
The volume numbers might be wrong. (Yup.)
By now they understood that different box volumes were due to different-sized corner squares. We zoomed in on this. I asked them to draw a 10 × 12 rectangle in their journals. We removed 1 × 1 corners and calculated the volume. Then 2 × 2. They kept going.
Then I gave them a fresh sheet of paper. We measured it — 28 cm by 21.5 cm — and I asked them to build a systematic table just like before. I said something like, “Now that you know how to figure out the volume without making the boxes, see if you can figure out what corner size will give you the maximum volume.”
I saw kids high-fiving: “The corner has to be 4 by 4!”
Rapha and Cristian were beaming. “That was one of the boxes we made!”
We ended class on that. I swore I felt myself tearing up.
On Monday we’ll play with this applet.
And we’ll ask Wolfram Alpha to take the derivative for us. I’m pretty sure the class could write the equation: V = (28 − 2x)(21.5 − 2x)(x).
I just tried it — WA says the optimal square side is approximately 4.01965. My kids got 4. Pretty damn good for 6th-grade brute-force math.
Now that I’m writing this, I think I’m most proud of how well the kids worked together. I paired them randomly — and got all the odd couples: high/low, shy/outgoing, squirrelly/quiet, jock/nerd, princess/cowboy.
Not one whine when names were called.
How did I get so lucky?